充要条件是高中数学中最重要的数学概念之一,这个概念是逻辑学的重要内容,是数学语言的重要组成部分,是数学表达和交流的工具。同时也是学生学习数学概念的重要思维工具。数学学习离不开数学定义和定理(判定定理和性质定理)的学习,而判定定理的本质就是寻找结论成立的充分条件,性质定理就是寻找结论成立的必要条件,而给数学概念下定义的本质就是找寻结论成立的充要条件。
一、充分条件和必要条件的概念
要理解充分条件和必要条件的概念,我们从一个实际的例子开始,这是我们学习和理解数学概念的重要方法。看到一个抽象的数学概念,我们首先应该想到的不应该是抽象的数学表达,而是去举出足够多的例子,然后再把所举的例子抽象成数学语言,这样,抽象的数学概念就变得具体而可触摸了。
古语有云:“水至清则无鱼”。在这里,“水至清”就是“无鱼”的充分条件,因为你让水“至清”,鱼就死了,但我们要让鱼死,还有很多方法。不给它吃的,可以饿死它;给它吃毒药,可以毒死它……等等,大家可以想想还有些什么方法。
回到刚才的问题,我们研究的是“无鱼”这个结果,所以有了很多的方法,“水至清”是其中的一种方法,它可以导致“无鱼”,因此是达到目的的一个充分不必要条件。但我们如果研究的是“水至清”这个结果,那么“无鱼”是它的一个必要不充分条件,因为如果有鱼,说明水没有“至清”,“无鱼”不一定是因为“水至清”,“无鱼”还可能是因为水被严重污染了。再比如:手机没电了,就不能开机。“手机没电”就是“手机不能开机”的充分条件,“手机不能开机”就是“没电”的必要条件,因为“能开机”,手机是一定有电的。这样的例子非常多,我们可以一直的举下去,你能举出的例子越多,就越有助于你理解这个概念,但最后一定要抽象成数学概念,用数学的语言表达出来。
课本上是这样定义充分条件和必要条件的。

在这个概念中,我们要注意以下两点:
(1)认清研究的对象(主元)是p还是q,即研究的是谁的充分条件和必要条件,也就是上面加红的部分。这是解决关于充要条件的题目的第一个步骤,在解题时很多同学会把充分和必要给弄反,其根源就在与没有去关心研究的是谁的充分性和必要性,只是去关心“前与后”,他们机械的认为,前推出后是充分,后推出前是必要,须知前与后是相对的。比如“x>1的充分条件是x>2”这里得出的就是后推出前,因为研究对象是“x>1”。
(2)必要条件的意义是:“p能推出q,说明如果q不成立,那么p一定不成,所以,q对p而言是必要的,因此q是p的必要条件。”必要条件指的是研究的对象(这里是p)可以推出什么,什么就是它的必要条件。
一般地,

在上面的定义中,研究对象都是q,因此,我们在处理充要条件的问题中,可以统一的把研究对象标示为q,这样,谁推出q,谁就是q的充分条件,因此找出q的一个充分条件就得到q的一个判定定理;q推出谁,谁就是q的必要条件,因此找出q的一个必要条件就得到q的一个性质定理;同样的,找出q的一个充要条件就得到q的一个定义方式。
这三个概念,我们还可以用以下的电路图来理解:
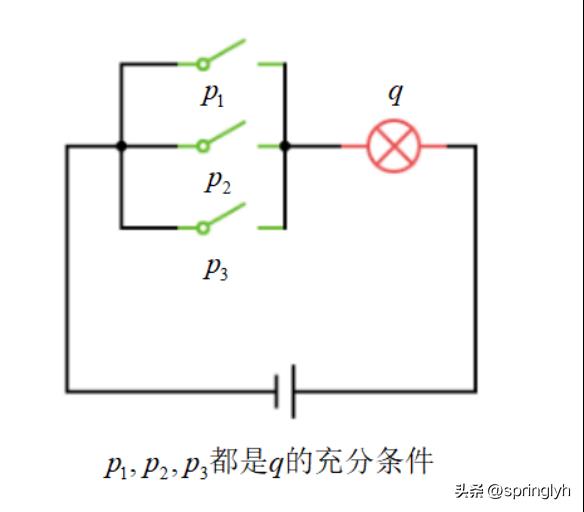
充分条件
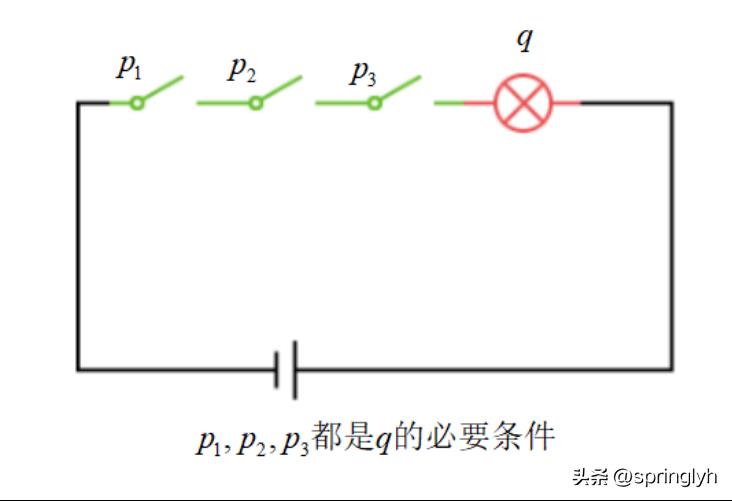
必要条件
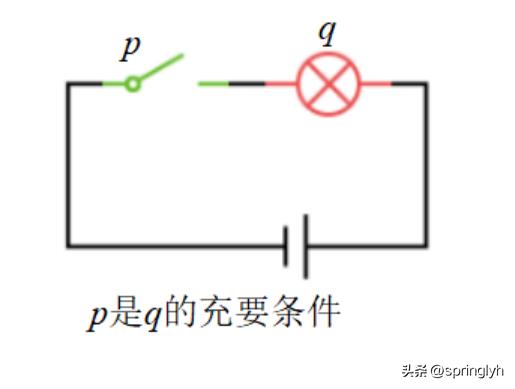
充要条件
二、充要条件的集合解释。
先看一个图形:
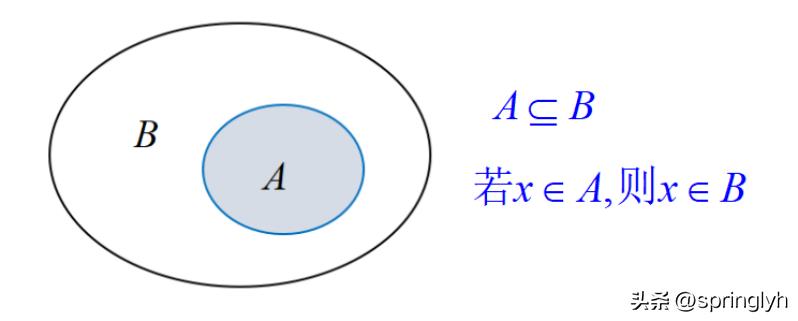
从这里我们可以得出一个结论:小范围⇒大范围,但大范围⇏小范围。
看一个数学的例子:x>1可以推出x>0,但x>0不可以推出x>1,因此x>1是x>0的充分不必要条件。
需要注意的是这里的大与小,是范围的大与小,即将其看成一个集合后,集合所包含的元素的多少,元素多就说明大,元素少就说明小。不是数的大小,否则上面例子中,1>0,但集合{x|x>1}比集合{x|x>0}小。
一般地,我们有下面的结论:

三、题型示例
【题型一】充分条件与必要条件的判断


因此在说明不成立时,都要尝试去举出反例,不论那个结果是多么的显而易见。举例子是高中生非常重要的一种能力,它可以让你把抽象的东西变得具体。


因此我们希望学生养成举例子的习惯,先通过分析元素的多少做出初步判断,再通过求出集合确认答案。这样一来可以减少出错的机会,二来可以培养学生的“数感”。




这种题型的解题步骤是:
(1)“认清q”,最好在题目中标示出来。
(2)“少推多”,先由范围的大小做出初步判断,再通过计算做出准确判断。
【题型二】充分条件与必要条件的应用



本题与【例1】的区别在于充分不必要与充分条件的区别,由于充分条件包括充分不必要条件和充要条件两种情况,而充要条件表示p与q等价,处理起来更简单,在这里即为两集合相等,因此我们只要思考两集合什么时候相等即可。

把这道题的方法归纳起来就是:对于“若p是q的充分不必要条件,求字母的取值范围”这样的问题,先处理问题1:“若p是q的充分条件,求字母的取值范围。”;然后再考虑问题2:“若p是q的充要条件,求字母的值。”问题2一般来说很简单,得出结果后,在问题1求出的范围中去掉问题2得到的值即可。但由于问题2很多时候是无解的,我们可以先判断问题2的解是否存在,如果不存在,问题1的答案就是我们要的答案。
类似的,在处理真子集问题时,我们也可以采用同样的方法。

在处理充分条件和必要条件的问题中,一定要注意“充分条件和必要条件(“是”,“的”)结构对比。看下面两道题:

这两种题型本质上没什么区别,重点其实是在认清q。题目1的q在后,题目2的q在前。
【题型三】充要条件的证明
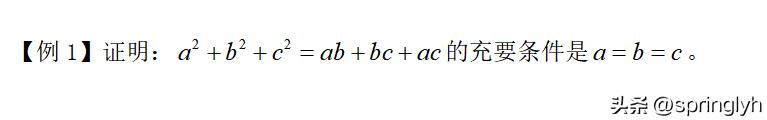
这是一个“的”型结构的问题,q在前面。

这样就证明完了充分性,这里我们要学习一种证明等式成立的基本方法,即“要证A=B,只需证明A-B=0”。下面证明必要性,这里要证明a=b=c,实际上是证明三个等式(a=b,b=c,c=a),如何从一个等式得到三个等式是思考的重点,所以我们想到一个重要的结论:几个非负数的和为零,那么每一个非负数都是零。从而构造出三个非负数的和的形式,于是就有了下面的方法:

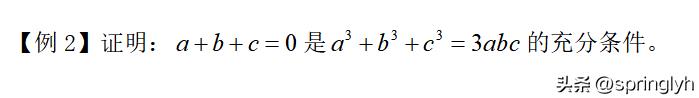
这是一个“是”型结构问题,q在后面。

这道题当然还可以通过直接把
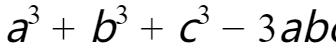
因式分解来处理。
四、一个有争议的问题
先看下面这道题(题目与答案均来自于《高中同步测控优化设计数学必修第一册》):

由于空集是任意非空集合的真子集,这个答案粗看似乎没什么问题,但我们把m=0代入原题,就得到如下结论:
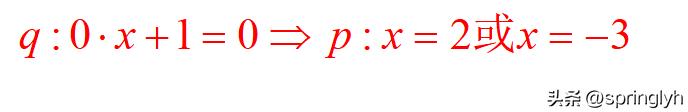
如果这个结论是对的,我们也就一定可以得到
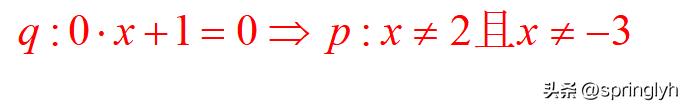
这显然是不合适的。所以我认为,在这里q对应的集合是不可以为空集的。这样的例子在很多教辅书上都有,答案基本也是包括空集的情形的。

写在最后
通过充分条件和必要条件的学习,我们需要去思考和体验这个知识背后存在的数学价值。
在观察现象、认识事物或处理问题时,“数学的方式”是与众不同的。
首先,我们的目标取向是:“追求最大限度的一般性模式特别是一般性算法”,而研究的起点是对具体事物(举例子,与学过的知识类比和联系等)进行数学抽象。
其次,数学的思考结构具有系统性、普适性,其基本套路是“具体的事物——抽象的数学对象——探索数学性质——构建知识体系”。
再次,数学的思维方式具有结构性、一致性、连贯性,包括:观察、分析、对比具体事物;抽象化;应用数学符号;建立数学模型;分析、推理、运算;改进、推广;更深入的洞察内在联系;在更大的范围内进行概括;建立更一般的统一的理论等。这是一套严谨的、行之有效的科学方法,是在获得数学知识体系中必须使用的思维方式。
最后,数学的表达方式具有统一性,是用一套全世界通用的符号形式在进行交流。
数学的思考结构、思维方式和符号化表达正是数学的力量所在,它逻辑性强,简明而准确,具有四两拨千斤的功效。
